What Is Homomorphic Encryption? An In-Depth Look at Zama’s Core Technology Principles

As data privacy protection receives increasing attention, especially in cloud computing, blockchain, and artificial intelligence scenarios, how to perform effective computation without exposing original data has become a major challenge.

Homomorphic Encryption, as an emerging cryptographic technology, provides the possibility of executing computations directly on encrypted data, finding a new balance between privacy protection and data usability. Recently, the project Zama, which focuses on this field, has received substantial funding and industry attention, pushing this technology from theory toward practical application.

What Is Homomorphic Encryption

Homomorphic Encryption is a form of encryption that supports performing operations on encrypted data (ciphertext), such that the decrypted result of the computation is identical to the result obtained by first decrypting and then computing. In other words, you can process ciphertext without knowing the original data content, and the final decrypted result will be the same as if the operation had been performed directly on plaintext.

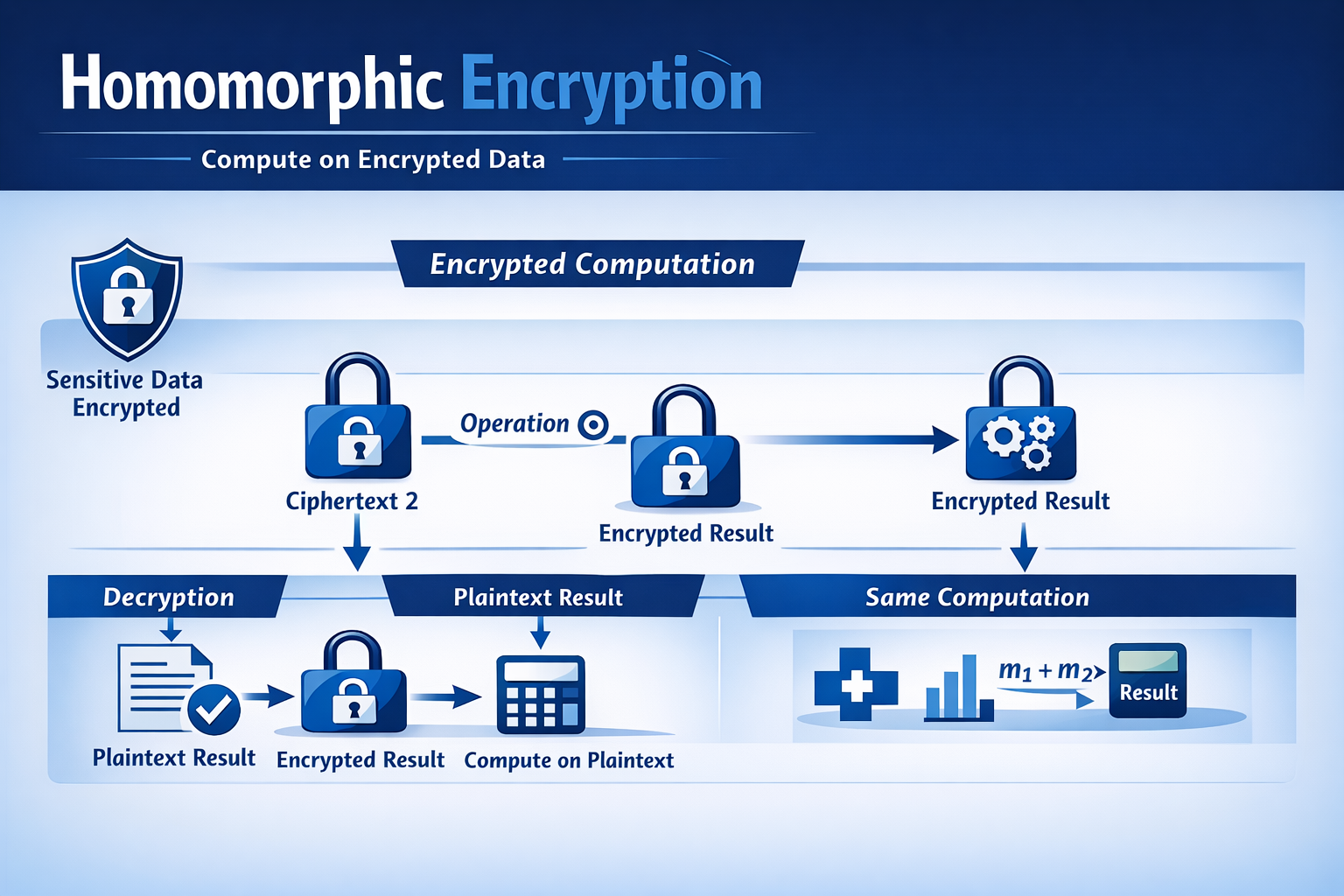
This technology is based on homomorphic properties in number theory and abstract algebra, allowing encrypted data to maintain its ciphertext structure while undergoing operations such as addition and multiplication. Its goal is to achieve “computable encrypted data”, fundamentally addressing the limitation of traditional encryption methods that require decryption before computation.

Why Traditional Data Encryption Cannot Participate Directly in Computation

Traditional encryption technologies (such as AES and RSA) primarily focus on the confidentiality of data during storage and transmission. They protect information by transforming data into a form that cannot be directly recognized. However, in practical applications such as data analysis and cloud processing, this encrypted data must be decrypted before it can participate in computation, in order to perform operations such as addition and multiplication. This means that third party servers or service providers can access plaintext data during computation, creating the risk of privacy leakage.

In simple terms:

• Traditional encryption protects the privacy of “static data”
• But it cannot keep data encrypted during “dynamic computation”
• Therefore, computation requires decryption, leading to data exposure risks

How Homomorphic Encryption Enables “Computable Encrypted Data”

The core of homomorphic encryption lies in the homomorphic nature of mathematical structures:

For an encryption function E and a decryption function D, if for two plaintexts m₁ and m₂ and a certain operation (such as addition or multiplication), the following holds:

D(E(m₁) ⊕ E(m₂)) = m₁ ✕ m₂

Then such an encryption method is homomorphic encryption. That is, when a certain operation (⊕) is performed on ciphertexts, the operation after decryption is still equivalent to the native operation (✕) between the plaintexts.

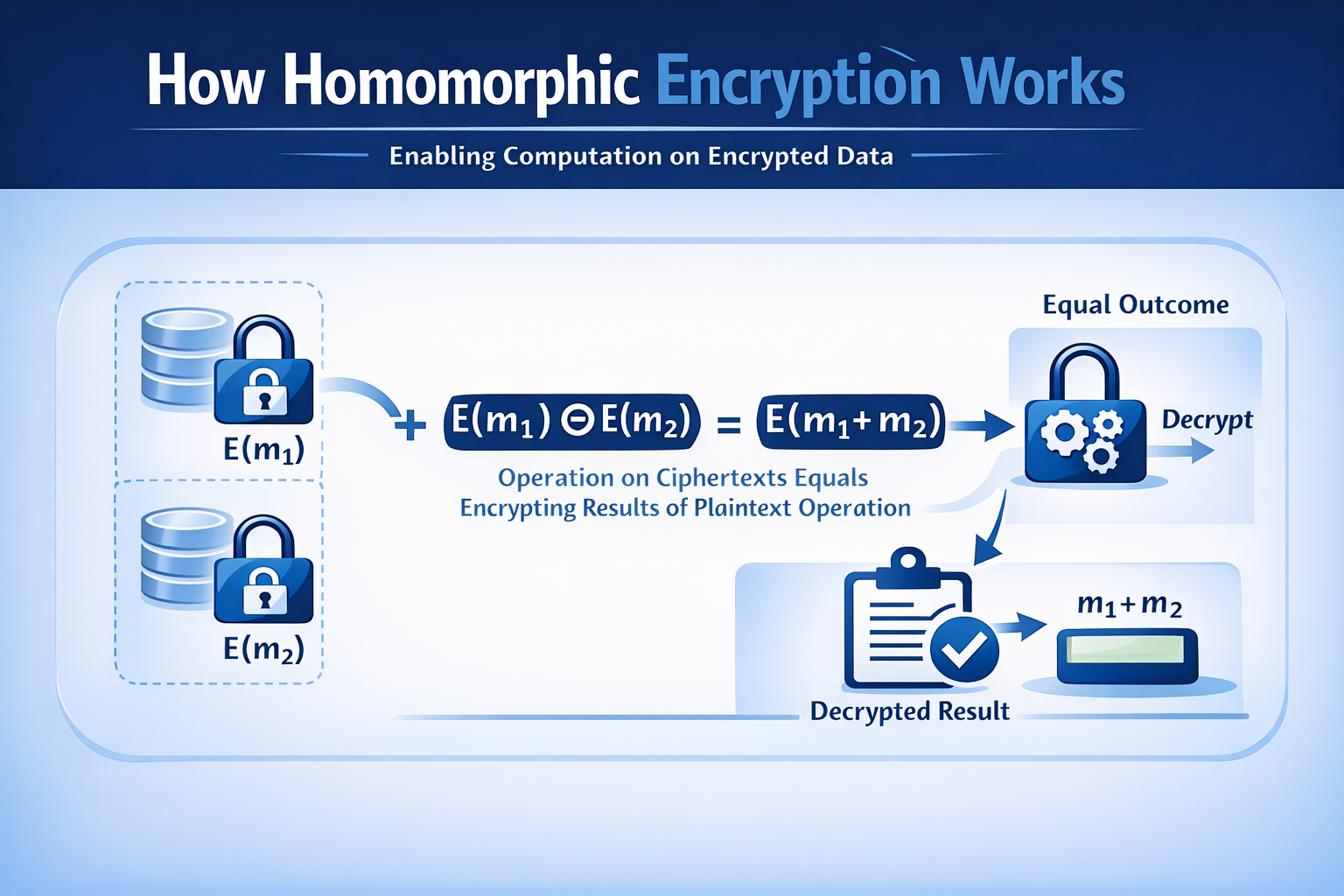
This property allows ciphertexts to perform complex computations without revealing the original data content, greatly enhancing privacy during data processing.

Differences Between Fully Homomorphic Encryption (FHE) and Partially Homomorphic Encryption

Homomorphic encryption can be classified by the range of operations it supports:

• Partially Homomorphic Encryption (PHE) Supports only one type of homomorphic operation, such as only addition or multiplication. For example, the Paillier cryptosystem supports additive homomorphism, while ElGamal supports multiplicative homomorphism. This mode can only perform limited types of operations and therefore cannot represent all computations.
• Fully Homomorphic Encryption (FHE) Supports arbitrary basic operations such as both addition and multiplication. This means that any logic circuit or program that can be represented as a combination of these operations can be executed in the encrypted state, making it a truly general homomorphic encryption scheme. FHE was long regarded as the “holy grail” of cryptography due to its enormous theoretical potential, but early implementations were difficult to make practical due to performance constraints.

How Zama Optimizes the Practical Efficiency of Homomorphic Encryption

One of the biggest obstacles to the practical application of homomorphic encryption, especially Fully Homomorphic Encryption (FHE), is its high computational cost. Because ciphertext operations involve complex algebraic structures and noise control mechanisms, early FHE implementations were far less efficient than plaintext computation, limiting their feasibility in real systems. As a result, recent homomorphic encryption research has gradually shifted its focus from theoretical feasibility to engineering optimization and system implementation.

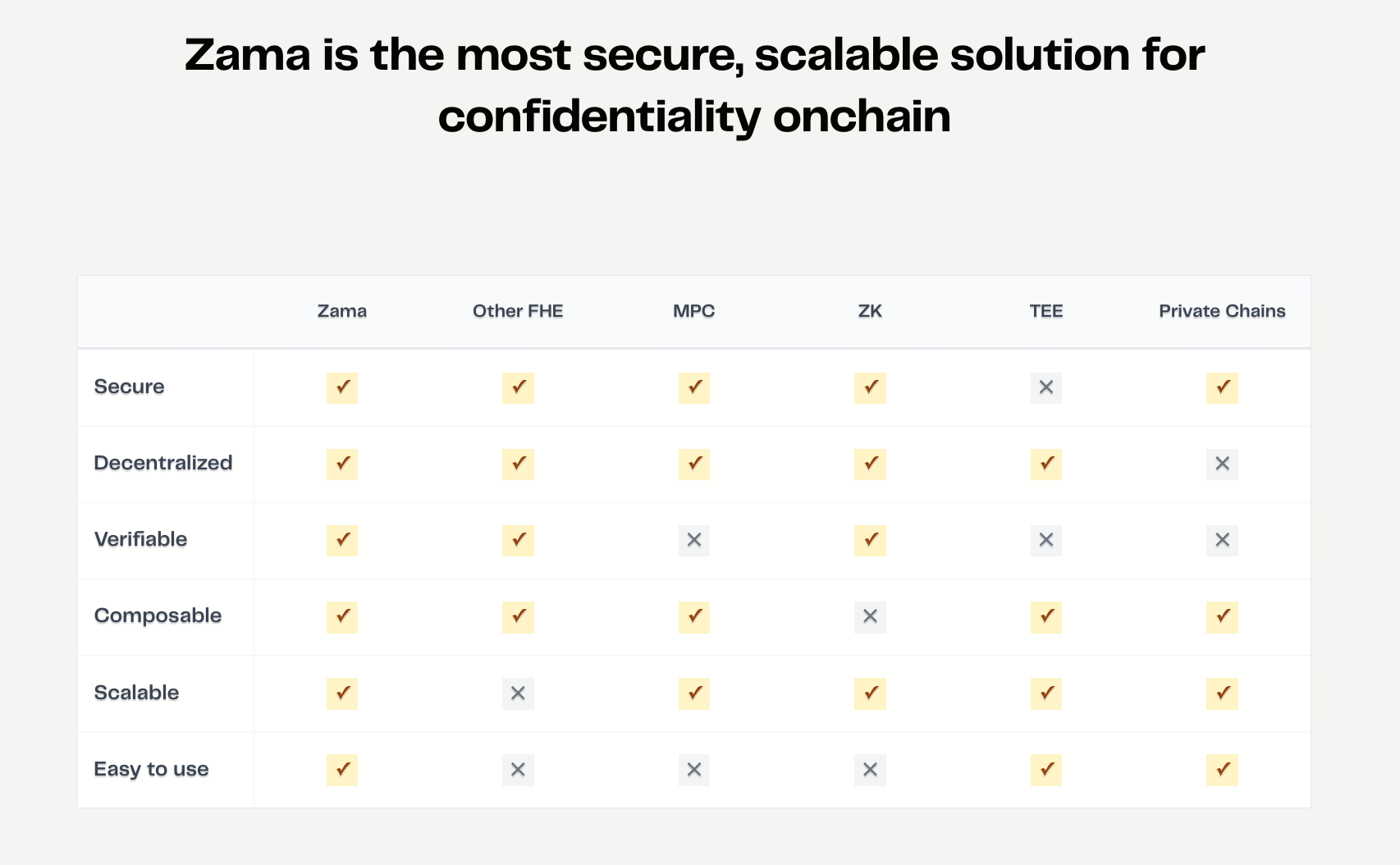
Image source: Zama

In this context, Zama primarily optimizes existing FHE schemes through engineering approaches rather than altering their underlying cryptographic assumptions. Its work focuses on key aspects such as ciphertext representation, computational circuit design, and noise growth control. By reducing unnecessary computational depth and intermediate overhead, Zama improves overall execution efficiency while maintaining security. These optimizations allow homomorphic computation to gradually achieve acceptable performance in certain application scenarios.

At the implementation level, Zama provides a series of open source FHE tools and libraries to support development needs at different levels. These tools encapsulate complex parameter selection and noise management logic at the lower level, enabling developers to use related functionality without deeply understanding the internal details of homomorphic encryption. At the same time, Zama is also attempting to introduce homomorphic encryption into more general computing environments, allowing encrypted data to participate in more complex program logic rather than being limited to single arithmetic operations.

In addition, given the computation intensive nature of homomorphic encryption, Zama is exploring integration with parallel computing architectures such as GPUs in the execution environment to alleviate performance bottlenecks in pure CPU environments. This approach of coordinated software and hardware optimization provides a realistic path for homomorphic encryption to achieve larger scale applications in the future and lays the foundation for further performance improvements.

Current Technical Challenges Facing Homomorphic Encryption

Although homomorphic encryption theory is mature and gradually moving toward practical use, significant obstacles remain:

1. High performance overhead: FHE operations are much slower than plaintext computation, which is a major bottleneck limiting large scale deployment. Hardware acceleration such as GPUs and ASICs can improve efficiency, but overall computational costs remain high.
2. Noise accumulation problem: Noise is generated during ciphertext computation, and excessive noise can cause decryption to fail. Techniques such as bootstrapping are required to reset noise, but this introduces additional overhead.
3. Type support and limitations: In some implementations (such as fhEVM in blockchain), only limited data types are currently supported, making it difficult to handle floating point numbers or complex data structures.
4. Standardization and ecosystem maturity: The level of standardization and ease of use of homomorphic encryption is relatively low, requiring more mature tools and protocols to support large scale development.

Which Industry Applications Homomorphic Encryption Is Transforming

The application scope of homomorphic encryption continues to expand, showing practical potential in multiple key industries:

1. Privacy computing and cloud services Users can send encrypted data to the cloud for computation without worrying about service providers accessing plaintext data, helping to protect data privacy and meet compliance requirements.
2. Blockchain and confidential smart contracts By executing encrypted operations on chain, new functionalities such as transaction privacy and confidential contract execution can be achieved. This is an important application direction of Zama Protocol.
3. Artificial intelligence and privacy preserving training Homomorphic encryption supports performing machine learning inference and even training in the encrypted state, providing privacy protection for sensitive user data.
4. Financial data processing From financial risk modeling to cross institution data analysis, homomorphic encryption can protect customer privacy while supporting complex computation.

Future Development Directions of Homomorphic Encryption

With deeper research and increased industry investment, homomorphic encryption may show the following trends in the future:

1. Performance improvement and integration with hardware acceleration Combining hardware designs such as GPUs, FPGAs, and ASICs with better algorithms and compiler improvements to achieve faster encrypted execution efficiency will be a key focus of technological development.
2. Cross domain protocol integration Homomorphic encryption may be combined with other privacy preserving technologies (such as zero knowledge proofs and MPC) to form more powerful and flexible privacy computing solutions.
3. Standardization and ecosystem improvement The industry will promote standardization of FHE specifications and build more developer tools, SDKs, and implementation libraries to make application development more convenient.
4. Large scale commercial deployment In the coming years, as performance bottlenecks are alleviated and industry demand grows, homomorphic encryption will enter more practical application scenarios, including Web3, medical data analysis, and cross institution data sharing.

Summary

As a revolutionary cryptographic technology, homomorphic encryption provides an important bridge between privacy and data usability by supporting computation in the encrypted state.

Compared with traditional encryption methods, it offers unique data protection advantages but also faces challenges such as performance and noise management. The project Zama, through algorithm optimization, execution acceleration, and practical protocol construction, holds a leading position in promoting homomorphic encryption from theory to real world application. As technology continues to mature and gain industry adoption, homomorphic encryption will continue to transform data processing across multiple industries and play an increasingly important role in the future of privacy computing.

FAQ: Common Questions About Homomorphic Encryption

Q1: Can homomorphic encryption be used in practice now? It can already be used in specific scenarios such as privacy computing and encrypted inference, but due to high performance overhead, it is still not suitable for all high frequency computation scenarios.

Q2: What is the difference between homomorphic encryption and zero knowledge proofs? Homomorphic encryption focuses on completing computation in the encrypted state, while zero knowledge proofs are used to prove the correctness of results. They address different problems.

Q3: What problems does Zama’s solution mainly address? Zama mainly lowers the barrier to using homomorphic encryption through engineering optimization and toolchains, and improves its usability in real systems.